How did the ancient Romans count with their fingers?

All the sources clearly state that there is no actual record of how Romans performed mathematical calculations. However it is well established that the Romans knew of, and used, the abacus.

It is also trivial to see how the Roman Numeral system was a literal representation of the results shown on the abacus in non-subtractive mode.

Finally, it is well established that accomplished abacus users exceeded even pocket calculator users well into the 1980's except for abstruse calculations, and Richard Feynman; but then Feynman seems to have been a perpetual exception.

"Raios cubicos!" he says with a vengeance. Cube roots! He wants to do cube roots by arithmetic. It's hard to find a more difficult fundamental problem in arithmetic. It must have been his topnotch exercise in abacus-land.

He writes down a number on some paper— any old number— and I still remember it: 1729.03. He starts working on it, mumbling and grumbling: "Mmmmmmagmmmmbrrr"— he's working like a demon! He's poring away, doing this cube root.

Meanwhile I'm just sitting there.

One of the waiters says, "What are you doing?".

I point to my head. "Thinking!" I say. I write down 12 on the paper. After a little while I've got 12.002.

The man with the abacus wipes the sweat off his forehead: "Twelve!" he says.

"Oh, no!" I say. "More digits! More digits!" I know that in taking a cube root by arithmetic, each new digit is even more work that the one before. It's a hard job.

He buries himself again, grunting "Rrrrgrrrrmmmmmm ...," while I add on two more digits. He finally lifts his head to say, "12.01!"

The waiters are all excited and happy. They tell the man, "Look! He does it only by thinking, and you need an abacus! He's got more digits!"

(Probably only Hans Bethe and Srinivasa Ramanujan "had more friends amongst the numbers natural, rational, and complex" than Feynman.)

Early in the project [Feynman and Bethe] were working together on a formula that required the square of 48. Feymnan reached across his desk for the Marchant mechanical calculator.

Bethe said, “It’s twenty-three hundred.”

Feynman started to punch the keys anyway. “You want to know exactly?” Bethe said. “It’s twenty-three hundred and four. Don’t you know how to take squares of numbers near fifty?”

Given these facts, there seems no reason to imagine or invent more complex calculation techniques that what we already to know the Romans to have possession of - an inexpensive, accurate and exceedingly efficient calculator that remains in use in Asia even today.

Today we are all taught in Grade School that both accuracy and precision of our answers is vital for marks. However in the real world answers are rarely calculable to infinite precision - and a couple of decimal places is often more than sufficient. The ancients well knew of the Secant Method for solving roots of functions, which requires no Calculus and converges rapidly, even if less so than Newton's Method. That is what Feynman is doing above in calculating cube roots - and it hardly matters for this purpose which of the two he uses as both will be much faster than even a Master of Abacus.

We would do our children a great service if we taught them younger the beauty of true Arithmetic, and that there are many different ways to evaluate each problem, depending on the precision required at the moment. I was fortunate to stumble on this myself, through reading, at a tender age.

Update - Repeating my comment below, expanding on my first paragraph:

I dismiss the entire notion (use of finger counting) as fantastical - a schoolboy prank gone wild. First, roughly a quarter of those finger positions are impossible on my hands without physically breaking fingers. Another quarter or so are extremely painful to hold. Then the thought of attempting to combine two such on the same hand is mind-numbingly terrifying. Then both hands at once - not happening.

Note: Non-subtractive mode is the representation of 4 as IIII instead of as IV; of 9 as VIIII instead of as IX; etc.

This page displays many Roman era testimonies that there was a system, and that it served to count at least up to the hundreds. I'll copy here the most important ones.

Juvenal in his Satire X, 246 251, referring to Nestor, famous in Antiquity for his longevity, clearly implies that units and tens were counted on the left hand and the hundreds were counted on the right hand:

The king of Pylos (Nestor), if any credibility you give to the great Homer, was an example of life as long as that of the crow. Hugely lucky he who avoided his death for so many centuries and already counts his years with the right hand and has drunk the new wine so many times!

In Apuleius' Apology, 89 , one finds convincing evidence in favour of the signs for 10, 30 and 40 (given that we can look at them in the picture), as well as a first-hand account of the difficulty of the system:

If you had said thirty years old instead of ten, we may have thought that you had made a mistake in the act of numbering and you had opened the fingers you should have had in a circle shape. But forty, which are easier than any other to be expressed with the opened palm, which you increase in a half, cannot be an error in the gesture of the fingers, unless, thinking that Pudentilla is thirty years old, you have counted them double because of the two consuls there are every year".

Also Quintilian in his Institutio Oratoria, I, 10, 35 makes this difficulty evident:

In the processes some tasks or questions to check the participants ´skills on the use of numbers are very common and in them they are considered ignorant not only those ones who hesitate or doubt on the sums, but those who fail on the account by the wrong or clumsy gesture of the fingers as well.

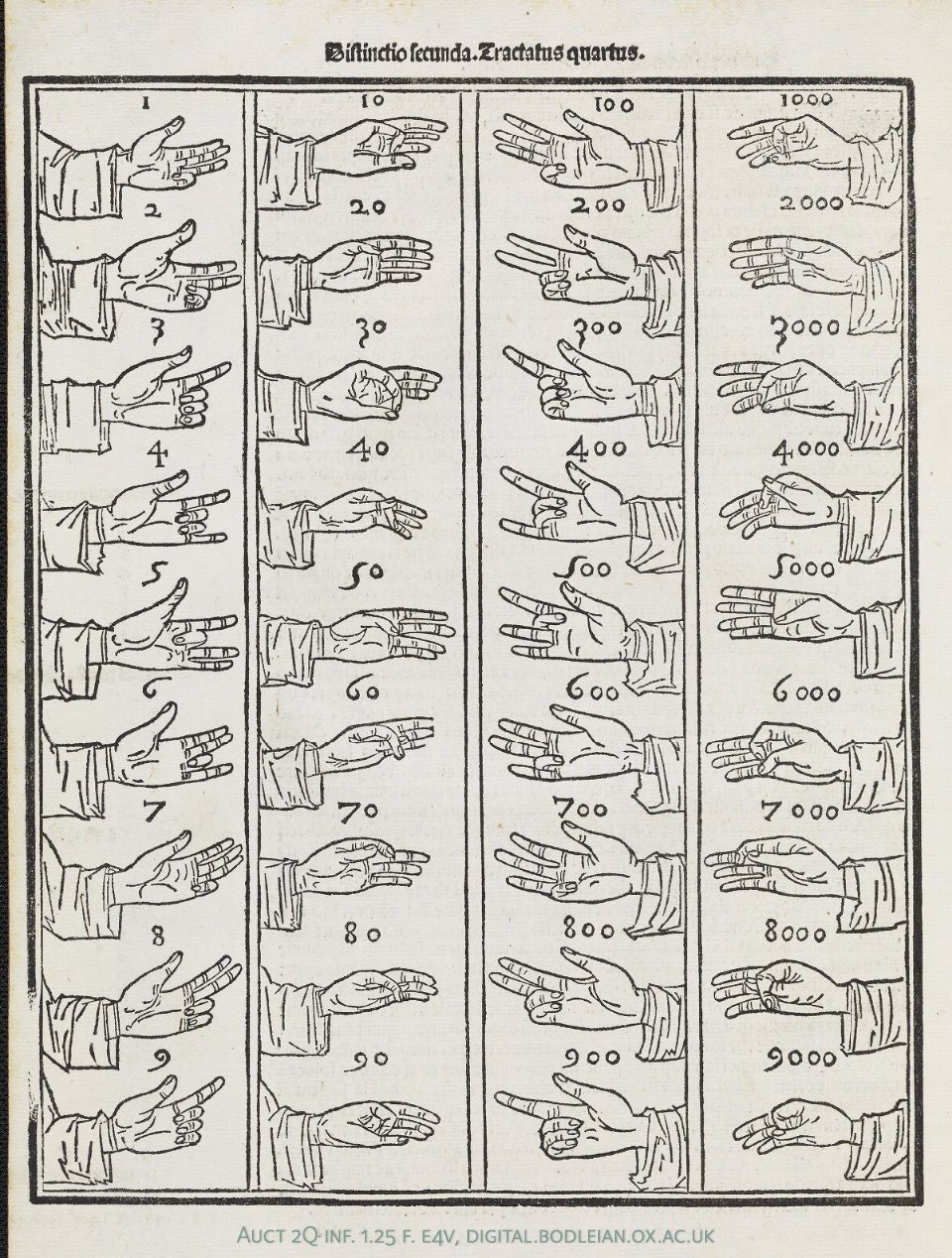
These three sources ought to make the picture more believable, and in fact, "it seems that St. Cyril of Alexandria (c. 376-444) in his Liber de computo (Calculating, Computing or Counting Book), chapter CXXXVIII, entitled De flexibus digitorum, III, 135 (about the positions of the fingers) provides us the earliest description of the system". So Bede's description owes to that. The following is an illustration present in the Distinctio secunda, Tractatus quartus of Luca Pacioli's Summa de Arithmetica, geométrica, proportioni et proportionalita (1494, Venice):

The earliest graphical representation is probably found in Rabanus Maurus' De Numeris (9th century):

It is also important to note there was one such system (the same?*) in Greece; Aristophanes refers to it, for example, in his comedy The Wasps (pages 655-663):

Bdelycleon (the one who hates Cleon).- Listen to me, dear little father, unruffle that frowning brow and reckon, you can do so without trouble, not with pebbles, but on your fingers.

According to Professor Michele Scolari's blog (Italian), an analogous system existed in Persia. It was described in the Persian dictionary Farhangi Djihangiri (XVI century), but Plutarch speaks of "finger calculations" at the court of the Persian King Artaxerxes III, who lived between the fourth and third century BC.

*Scolari suggests that indigitatio, the art of counting with fingers, originated in Egypt - traces of it can be seen in a group of scultures (which he calls Censimento del bestiame ("Livestock census"), though I'm failing to identify this group or at least its English name) displayed at the Egyptian Museum in Cairo - and then spread to the Greco-Roman and Persian worlds.

Alberto Angela in his A day in the Life of Ancient Rome gives credit to the system, giving (Italian) another depiction of it as well as stating that a consequence of this counting system can be seen still today, in how people count in some souks in the Arab world.

Angela states that numbers up to 10000 could be expressed with fingers, combining the two hands. But obviously a number like 1234 would be expressed in 4 steps, not (impossibly) all at once albeit with the two hands, as the other answer misleadingly puts it. Given that the Romans read from left to right and wrote numbers starting from the largest "digit" (like MCCXXXIIII), it's safe to say the steps would be: first, make the sign for 1000 with your right hand; then, make the sign for 200 with that same hand; then make the sign for 30 with your left hand, and finally make the sign for 4 again with your left hand.